A red-black tree is a binary search tree with one extra bit of storage per node: its color, which can be either RED or BLACK.
A binary search tree is a red-black tree if it satisfies the following red-black properties:
1. Every node is either red or black.
2. The root is black.
3. Every leaf (NIL) is black.
4. If a node is red, then both its children are black.
5. For each node, all paths from the node to descendant leaves contain the same number of black nodes.
By the red-black properties above, red-black trees make good search tree. It can been proved that a red-black tree with n internal nodes has height at most 2 lg(n + 1). Since the dynamic-set operations Search, Minimum, Maximum, Successor, and Predecessor can be implemented in O(lg n) time on red-black trees.
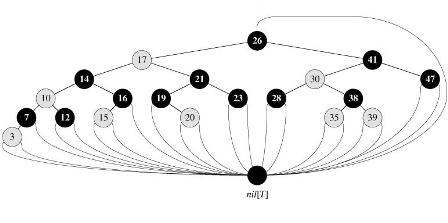
As a matter of convenience in dealing with boundary conditions in red-black tree code, we use a single sentinel to represent NIL. This sentinel nil[T] represent all the NIL’s-all leaves and the root’s parent. See the picture below:
Here is the class template of red-black tree I have designed.
enum cotype {red, black};
template<typename T>
class BRTreeNode
{
public:
BRTreeNode(T d, cotype c=red, BRTreeNode<T> *p=NULL,
BRTreeNode<T> *l=NULL,BRTreeNode<T> *r=NULL)
:color(c),data(d),parent(p),left(l),right(r) {}
T data;
cotype color;
BRTreeNode<T> *parent;
BRTreeNode<T> *left;
BRTreeNode<T> *right;
};
template<typename T>
class BRTree
{
public:
BRTreeNode<T>* m_root;//the root of the tree
BRTreeNode<T>* nil;//nil is a sentinel.
// a function pointer that points the visit function
typedef void (*v_func)(const T &data);
v_func m_visit;//the visit function pointer
BRTree(v_func f,BRTreeNode<T>* p=NULL):m_root(p),m_visit(f)
{//construct a Black-red tree
nil = new BRTreeNode<T>(0,black);
nil->left=nil->right=nil->parent = NULL;
}
//Insert an element into the tree
void Insertion(const T&);
//Delete an element from the tree
BRTreeNode<T>* Delete(BRTreeNode<T>* );
//inorder tree walk, thus prints a sorted list
void InorderWalk() { Inorder(m_root);}
protected:
bool LeftRotate(BRTreeNode<T>* );//left rotation on a node
bool RightRotate(BRTreeNode<T>* );//right rotation on a node
void Inorder(BRTreeNode<T> *);//Inorder traversal of the tree
private:
};
The operations INSERT and DELETE, when run on a red-black tree with n keys, take O(lg n) time. Because they modify the tree, the result may violate the red-black properties. To restore these properties, we must change the colors of some of the nodes in the tree and also change the pointer structure.
We change the pointer structure through rotation, which is a local operation in a search tree that preserves the binary-search-tree property. The following figure shows the two kinds of rotations: left rotations and right rotations.
template<typename T>
bool BRTree<T>::LeftRotate(BRTreeNode<T>* x)
{//left rotation on the node x;
if(x->right!=nil)
{
BRTreeNode<T>* y = x->right;
x->right = y->left;//Turn y's left subtree into x's right subtree
if(y->left!=nil)//if y has left child, make its parent be x
y->left->parent = x;
y->parent = x->parent;//Link x's parent to y
if(y->parent==nil)
m_root=y;//make y be the new root
if(x->parent->left==x)
x->parent->left=y;
if(x->parent->right==x)
x->parent->right=y;
y->left=x;//Put x on the y's left;
x->parent=y;
return true;
}
else
{
cout<<"Left rotate failed because of right child is nil"<<endl;
return false;
}
}
template<typename T>
bool BRTree<T>::RightRotate(BRTreeNode<T>* x)
{
if(x->left!=nil)
{
BRTreeNode<T>* y = x->left;
x->left = y->right;//Turn y's right subtree into x's left subtree
if(y->right!=nil)//if y has right child, let its parent be x
y->right->parent = x;
y->parent=x->parent;//Link x's parent to y
if(y->parent==nil)
m_root=y;//make y be the new root
if(x->parent->left==x)
x->parent->left=y;
if(x->parent->right==x)
x->parent->right=y;
y->right=x;//Put x on the y's right
x->parent=y;
return true;
}
else
{
cout<<"Right rotate failed because of left child is nil"<<endl;
return false;
}
}
Insertion of a node into an n-node red-black tree can be accomplished in O(lg n) time. The first step is insert the node x into the tree red-black T as if it were an ordinary binary search tree and then we color x red. To guarantee that the red-black properties are preserved, we then recolor nodes and perform rotations. (the second part of Insertion procedure). See the following code:
template<typename T>
void BRTree<T>::Insertion(const T& data)
{//the first part is same as in BSTree
BRTreeNode<T>* x=m_root,*y=NULL;
if(!x)//the tree is empty
{
x= m_root = new BRTreeNode<T>(data,red,nil,nil,nil);
m_root->parent=nil;
}
else
{
while(x!=nil)
{
y=x;//store x's parent;
if(data > x->data)
x=x->right;
else
x=x->left;
}//now y is the insertion node's parent
x = new BRTreeNode<T>(data,red,nil,nil,nil);
x->parent=y;
if(data > y->data)
y->right=x;
else
y->left=x;
}
//the second part is to restore the red-black properties
while (x->parent->color==red)
//ensure there is no violation of property 4 and x is not the root
{//case 1: x's parent is its grandparent's left child.
if(x->parent==x->parent->parent->left)
//x->parent->parent always exits because x cannot be the root
{
if(x->parent->parent->right->color==red)
{//case 1.1: x's uncle is red
x->parent->color=black;
x->parent->parent->right->color=black;
x->parent->parent->color=red;
x=x->parent->parent;// now x is the grandparent
}//end of case 1.1
else
{//case 1.2: x's uncle is black
//case 1.2.1: x is right child
if (x==x->parent->right)
{
x=x->parent;
LeftRotate(x);
}
//case 1.2.2: x is left child
x->parent->color=black;
x->parent->parent->color=red;
RightRotate(x->parent->parent);
//end of case 1.2
}
}//end of case 1
else//case 2 (symmetry with case 1 with left and right exchanged)
{
if(x->parent->parent->left->color==red)
{//case 2.1
x->parent->color=black;
x->parent->parent->left->color=black;
x->parent->parent->color=red;
x=x->parent->parent;// now x is the grandparent
}//end of case 2.1
else
{//case 2.2
if (x==x->parent->left)
{//case 2.2.1
x=x->parent;
RightRotate(x);
}
//case 2.2.2
x->parent->color=black;
x->parent->parent->color=red;
LeftRotate(x->parent->parent);
//end of case 2.2
}
}//end of case 2
}
m_root->color=black;
}
It is apparently that properties 1, 3, and 5 hold when the second part of Insertion procedure is called.
There are actually 2 cases to consider in the while loop, but the two cases are symmetric, depending on whether x’s parent p[x] is a left child or a right child of x’s grandparent p[p[x]]. The node p[p[x]] exists, since if p[x] is the root, then p[x] is black. Since we enter a loop iteration only if p[x] is red, we know that p[x] cannot be the root. Hence, p[p[x]] exists. However, the subcase is divided based on whether x’s uncle’s color.
Let me explain the above code:
Case 1: x’s parent is its grandparent’s left child.
Case 1.1: x’s uncle is red
In this case, both p[x] and x’s uncle are red. Since p[p[x]] is black, we can color both p[x] and x’s uncle black, thereby fixing the problem of x and p[x] both being red, and color p[p[x]] red, thereby maintaining property 5. We then repeat the while loop with p[p[x]] as the new node x. The pointer x moves up two levels in the tree.
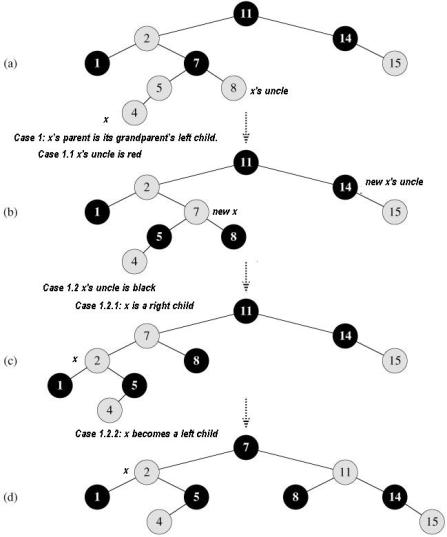
Let’s assume that x′ is the new x in the above figure. We will have 2 conclusion:
a. If node x′ is the root at the start of the next iteration, then case 1.1 corrected the lone violation of property 4 in this iteration. Since x′ is red and it is the root, property 2 becomes the only one that is violated, and we will terminate the loop and correct the lone violation by the last statement of this procedure.
b. If node x′ is not the root at the start of the next iteration, then case 1.1 has not created a violation of property 2. Case 1 corrected the lone violation of property 4 that existed at the start of this iteration. It then made x′ red and left p[x′] alone. If p[x′] was black, there is no violation of property 4. If p[x′] was red, coloring x′ red created one violation of property 4 between x′ and p[x′]. We will deal with this violation in Case 1.2.
Case 1.2: x’s uncle is black
There two situations distinguished by whether x is a right or left child of p[x] in this case. If node x is a right child of its parent (Case 1.2.1), we immediately use a left rotation to transform the situation into case 1.2.2, in which node x is a left child. As in case 1, property 4 is violated in either case 1.2.1 or case 1.2.2 because x and its parent p[x] are both red. In case 1.2.2, we execute some color changes and a right rotation, which preserve property 5, and then, since we no longer have two red nodes in a row, we are done. The body of the while loop is not executed another time, since p[x] is now black.
Because node x is not the root in case 1.2.1 and case 1.2.2, we know that there is no violation of property 2. Case 1.2.1 and case 1.2.2 do not introduce a violation of property 2, since the only node that is made red becomes a child of a black node by the rotation in case 3. Case 1.2.1 and case 1.2.2 correct the lone violation of property 4, and they do not introduce another violation.
The above figure shows the whole second part of Insertion procedure. (a) is a node x after insertion. Since x’s parent is its grandparent’s left child, case 1 is applied. Since x and its parent p[x] are both red, a violation of property 4 occurs. Since x’s uncle is red, case 1.1 in the code can be applied. Nodes are recolored and the pointer x is moved up the tree, resulting in the tree shown in (b). Once again, x and its parent are both red, but x’s uncle is black. Since x is the right child of p[x], case 1.2.1 can be applied. A left rotation is performed, and the tree that results is shown in (c). Now x is the left child of its parent, and case 1.2.2 can be applied. A right rotation yields the tree in (d), which is a legal red-black tree. However, the Case 2 section of the code is is just like case 1 with left and right exchanged.