Counting sort assumes that each of the n input elements is an integer in the range 0 to k, for some integer k. When k = O(n), the sort runs in Θ(n) time. Seems so fast? The answer is no. It just uses extra space to cut down the runtime. However I have extended the range to -k to k in the following implementation.
The basic idea of Counting sort is determine, for each input element x, the number of the elements less than x. Then what this number x represents? For example, if there are 17 elements less than x, then x belongs in output position 17(start from position 0). Here we use the array c to maintain this information. For instance, c[x]=17. This scheme must be modified slightly to handle the situation in which several elements have the same value, since we don’t want to put them all in the same position. In this situation we just decrement c[a[i]] (in my implementation is c[a[i]+k], which handle the negative number situation) each time we place a value a[i] into the b array. This causes the next input element with a value equal to A[i] to go to the position immediately before A[i] in the output array.
/*a[] is the unsorted array, b[] is used to store
the sorted array, k is the range of the given unsorted
numbers, for example, k equal 9 represents -9~9.
*/
void counting_sort(int a[],int b[],int k,int size)
{
int i=0;
int* c = new int[k*2+1];
memset(c,0,4*(k*2+1));
for(i=0;i<size;i++)
c[a[i]+k]++;//since the a[i] maybe lower than 0,
//here we plus k to avoid the index lower than 0;
//now c[i+k] contains the number of elements equal to i
for(i=1;i<k*2+1;i++)
c[i]=c[i-1]+c[i];
//C[i+k] now contains the number of elements
//less than or equal to i
for(i=size-1;i>=0;i--)
{
b[c[a[i]+k]-1]=a[i];
c[a[i]+k]--;
}
}
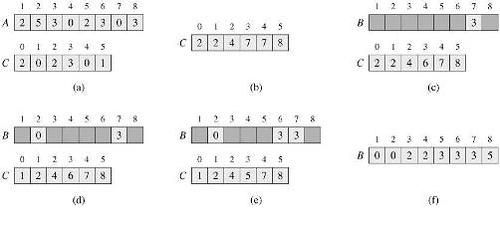
The following figure illustrates the counting sort. However, it only contains nonnegative elements in the input array A. figure (a) illustrates the c array after the first for loop has been executed. figure (b) illustrates the C array after the second for loop. (c)-(e) The output array B and the auxiliary array c after one, two, and three iterations of the third loop respectively. Only the lightly shaded elements of array B have been filled in. (f) The final sorted output array B.