Unlike the mergesort and quicksort, heapsort doesn’t require massive recursion or multiple arrays to work and the time complexity of heapsort is O(n log(n)) . It utilizes a special data structure called heap. Before we take a look at the Heap sort algorithm, let’s explain the the (binary) heap data structure.
Heap is an array object that can be viewed as a nearly complete binary tree. In my implement, I use an array to represent a heap. So the left child of an element a[i] is a[i*2]. Similarly, the right child of a[i] is a[2i+1]. And the parent is a[i/2].
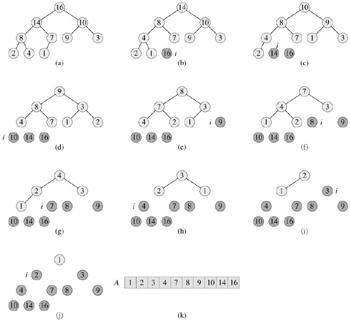
There are two kinds of binary heaps: max-heaps and min-heaps. In both kinds, the values in the nodes satisfy a heap property, the specifics of which depend on the kind of heap. In a max-heap, which is used in the heapsort algorithm, the max-heap property is that every node a[i]’s parent is larger than a[i] itself. Thus, the largest element in a max-heap is stored at the root. The following figure shows a max-heap as a binary tree and the array corresponding it.
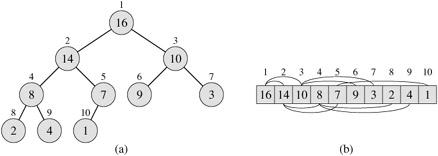
The heapsort begins by building a heap out of the data set, and then exchange the root(largest item) with the last item in the array and remove the last item from the heap. After remove the last item, it reconstructs the heap and exchange the largest it with the last item and do the same thing above. This is repeated until there are no items left in the heap.
To build a heap, we need a procedure Max_heapify to Maintain the heap property
Max_heapify is a important subroutine for manipulating the max-heaps. When Max_heapify is called, it is assumed that the subtree rooted at left child and right child of current item (a[i]) are max-heaps already. But that a[i] may be smaller than its children, thus violating the max-heap property. The function of Max_heapify is to let the a[i] “float down” in the max-heap so that the subtree rooted at index i becomes a max-heap. Please note that here a[0] is not be used here.
void Max_heapify(int a[], int i, int size)
{
while(i<=size)
{
int bigger=i;
if (i*2 <=size && a[i*2] > a[i])
bigger = i*2;
if (i*2+1 <=size && a[i*2+1] > a[bigger])
bigger = i*2+1;
if (bigger!=i)
{
a[i]^=a[bigger];a[bigger]^=a[i];a[i]^=a[bigger];
i=bigger;
}
else if (bigger==i)
break;
}
}
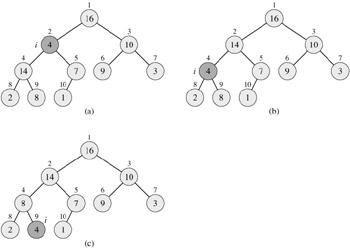
The following figure illustrates the action of Max_heapify. At each iteration, the largest of the elements A[i], A[i*2], and A[i*2+1] is determined, and its index is stored in bigger. If A[i] is largest, then the subtree rooted at node i is a max-heap and the iteration terminates. Otherwise, one of the two children has the largest element, and A[i] is swapped with A[bigger]. Now the a[i] float down a stage and the iteration is ended when a[i] reached the bottom of heap or a[i].
Here is another way to implement this procedure using recursion.
void maxheapify2(int a[], int i, int size)
{
int bigger=i;
if(i*2 <=size && a[i*2] > a[i])
bigger = i*2;
if(i*2+1 <=size && a[i*2+1] > a[bigger])
bigger = i*2+1;
if(bigger!=i)
{
a[i]^=a[bigger];a[bigger]^=a[i];a[i]^=a[bigger];
maxheapify2(a, bigger,size);
}
}
We can use the procedure Max_heapify in a bottom-up manner to convert an array A[1…size] into a max-heap. Since the elements in the subarray a[(⌊size/2⌋+2) …size] are all leaves of the tree, we can just start our procedure at the index of size/2.
The algorithm starts by using build_maxheap, After doing this, the max element is stored at he root a[0]. We exchange it with a[size] and decrease the size of the heap by 1. Now the children of the root remain max-heaps, but the new root element may violate the max-heap property. The solution is call Max_heapify to adjust the subarray a[0…size-1] to a heap. The heap sort algorithm then repeats this process for the subarray a[0…size-2] down to a[0…1].
void heapsort(int a[], int size)
{
int i;
for(i=size/2;i>=1;i--)
Max_heapify(a,i,size);
for(i=size;i>=2;i--)
{
a[1]^=a[i]; a[i]^=a[1]; a[1]^=a[i];
maxheapify2(a,1,i-1);
}
}
The following figure shows an example of the operation of heap sort after the max-heap is initially built.